简单物理竞赛题详解——有关电荷

引言

这里列出一道高考生也可简单解出的物理竞赛题，直接上题吧——

题目

两根无限长的均匀带电的电介质线，在空间沿两条交叉成十字形的相互垂直的直线分布，线上电荷线密度为σ，求两根线的相互作用力。可以认为线非常细并且未发生电荷重新分布。

注：“电介质线”指其上为非自由电荷。

解题

第一步

首先先推导一个公式：

2E·∆S=q/ε₀=4πkq=4πkσ·∆S

因此，

E=2πkσ

第二步

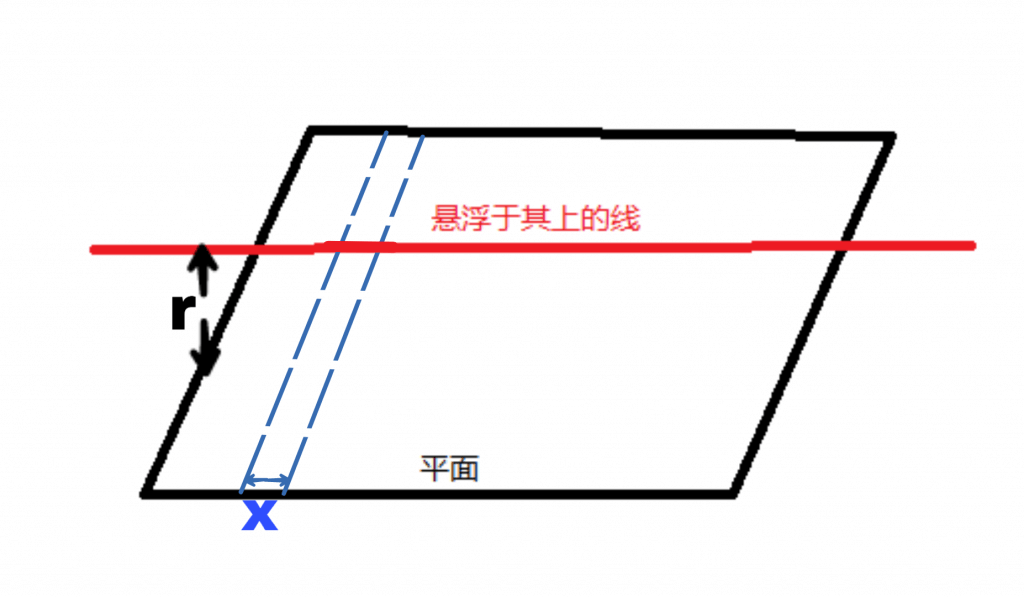
不妨引入一无限长带电平面模型，设其为一个边长为a的正方形，其电荷面密度为ρ；上方有一电介质线，长度l=a，电荷线密度为σ，距板高度为r。将板分成许多非常小，宽度为Δx的小条。如图:

则有

Δxρ=σ

（量纲法易证）

将这一条线看作无数点电荷，可得

F=∑Eq=2πkρ·∑qi=2πkρ·σl

=2πk(σ/Δx)·σl①

设这一条线上有N个点电荷，则

N=l/Δx

代入①，

F=2πkσ²·N

又因为a→∞，则每个Δx对上方的线作用力相同，所以，每一点受力

f=F/N=2πkσ²

本文部分内容参考了竞赛教辅资料。